The power of random: the Monte Carlo method

Hello again! Today, I have randomly decided to start writing some posts again after having been away for some time. This absence was not intentional, mind you; I used a coin-flip to decide if I was going to post that day for the last few weeks, and it just happened to land tails every time up till now. Speaking of randomness, welcome to my new column: “The power of random”, where I explore the near infinite things you can do with random numbers. In this arbitrary post, we look at the Monte Carlo method, and its various uses in numerical physics.

Sweet fortune at Monte Carlo

The year is 1946, and Stanisław Ulam was working on nuclear weapons at Los Alamos, the primary American laboratory for nuclear physics. While playing a game of solitaire, an interesting question popped up: what is the probability that any laid out game of solitaire will come out successfully? After cracking his mental knuckles and taking some time to come up with a solution, he eventually thought up a more efficient way to solve this problem. Why not play 1000 games of solitaire, and count the amount of games that are winnable?

You see, computers where an emerging technology back then, and as such, scientists like our friend Ulam where caught in the middle of a rapid increase in computational power. Although playing 1000 games of solitaire would be a scientific method reserved for the hopelessly bored back then, he could foresee that future computers would be able to simulate such games in a jiffy.

And thus, one of the first computer-based methods for physics was born. You would simply take an huge amount of random samples of whatever you wanted to measure, and mean over the outcomes. Of course, this technique would not be limited to only modelling games of solitaire, and thus nuclear work being done using this method would need a codename. The method was soon dubbed the ‘Monte Carlo’ method, named after the famous casino in Monaco because of the ‘gambling’ used to acquire your results, and the rest is history.

Law of large numbers

Ok, so we’ve got this cool new method to use to do some interesting physics, but how exactly does it work? Well my dear friend, it all starts with something we in the business like to call the ‘Law of large numbers’. To view this, we will first define some terms (in a semi-formal way, so bear with me):

Random variable: a function, usually called X, that assigns a measurable quantity to every possible outcome

For example, the random variable for heads or tails could be a function that takes heads, and assigns it to the number 1, and then takes tails, and assigns it to the number 0. When we encounter a random variable, like a coin-flip, we will probably want to know what to expect from its behaviour. For this, we can take a look at expected values.

Expected value: the weighted average of all elements in a random variable, usually called E(X)

This means that the expected value gives us an average, not the value you would expect to get when you take a sample. To get the expected value, you take each element multiplied by its respective probability, and then divide by the number of elements you have taken. If you want to take the expectation value, then, you would need to know the probability of each outcome. Most often, however, there are near infinite elements in our random variable, and the probabilities are not known beforehand. Law of large numbers to the rescue!

Law of large numbers: The average of a large number of trials will closely resemble the expected value

What this means is that we do not need to know exactly how a system behaves. As long as we just brute force a large number of measurements, we will eventually obtain the expected value! This is exactly what Ulam based his Monte Carlo method on. If you take enough random samples, you will eventually reach the right conclusion. This law is also why we try to take as many measurements as possible when doing an experiment. Because of the law of large numbers, the more measurements you take, the more accurate your results will be.

A slice of pi with Monte Carlo

So, now that we know why we can use random numbers, let’s look at the nitty gritty of the Monte Carlo method.

To apply the Monte Carlo method, you need 4 things:

• A domain to generate your random numbers in
• Some probability distribution that decides the weight of your random numbers. For ease of use, this probability distribution is mostly uniform
• Some calculation to use on the generated numbers, for example plugging the number into a function
• A way to interpret the results.

In general, for any Monte Carlo method, we repeat the same process over and over again. First you generate a number within your range, then you do some calculation on this number, and finally you process your result. You repeat this numerous times, until you are satisfied with the precision of your result.

For a coin flip for example, you generate randomly a 0 or a 1, and then take the mean of your sampling after many trials. You will eventually end up with a mean value of around ½.

Let me demonstrate more clearly how Monte Carlo may be used with the irrational number pi. Per definition, pi is the ratio between the circumference and the diameter of a circle. The area of a circle can also be expressed by the circumference, and equals pi for a circle with a radius of 1. Let’s look at only a quadrant of this circle, as shown below:

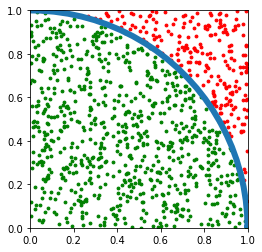
Here, we can see green dots lying inside of the circle quadrant, and red dots lying outside of it. Because the area of the square is precisely 1, the ratio between the dots inside of the circle to the total amount of dots will be equal to the ratio between the area of the circle to the area of the square for a large number of dots (law of large numbers). This ratio r = pi/4  : 1, so if we calculate 4r, we get approximately pi.

So, for our steps, we:

• Generate two numbers, x and y, in a range [0,1] with equal probability.
• Check if the coordinate lies within the circle, i.e. the distance from the origin is less than 1.
• Count all values inside of the circle, multiply by 4, and divide by the amount of measurements done. This will give us the ratio.

Epic! With this algorithm, we have now used our first Monte Carlo method. If you want to try this in your own programming language, the pseudo-code goes as follows:

N = 10000 //large number
pi = 0  //starting approximation of pi
counter = 0

while counter < N
{ 
	x,y = generate_random_number(range=[0,1], amount = 2)
	if sqrt(x**2 + y**2) <= 1
		pi += 4/N

	counter += 1
}

Making use of the Monte Carlo method

To wrap things up, let’s look at some specific implementations and use cases of the Monte Carlo method to broaden our understanding even further.

Monte Carlo integration

First, I shall name the specific variant we just used to approximate pi. This is what we call Monte Carlo integration. It is based on the fact that you have some prior knowledge about the function you want to integrate, because you either know the boundaries of the function (as was the case for our circle), or the function itself (as may be the case if you are given some function f(x)).

In the first case, you use the fact that a random sampling over some area with defined boundaries contained inside of another area will yield their ratio. Filling the space with dots is almost akin to filling in a large drawing, and then measuring how much ink each part of your drawing contains.

In the case of a known function, we take a random number x, and calculate f(x) numerous times. The average of this sampling will then be the average value of this function over the domain you are integrating over. Afterwards, you assume the integral to be a rectangle with the height being this average value, and the base width being your domain, and this will be your approximation of the integral.

Importance sampling

Of course, taking this average value may not be the best way for one to integrate. Say we have an integral where one value blows up, for a given x-coordinate, while the rest of the graph is relatively flat. Even though this extremely high value of x should dominate the expectation value, and thus contribute a large amount to the integral, it is only one point on the graph compared to nearly millions of other points that can be drawn from. By simply using the Monte Carlo integration, you are very likely to simply miss this value, and get a completely screwed up result.

In order to combat this, we use importance sampling. We assign a certain weight function, that decides with what probability we should draw our random values of x. In the specific case of a large peak, we may want a weight function that has a higher probability to draw values from the peak as compared to the flatter parts of the graph. In doing so, the wave function will take on the rough shape of the function we want to integrate over. This way, the results become more trustworthy, especially for lower sample sizes.

Metropolis-Hastings algorithm

Lastly, let’s discuss the case where we want to do some statistical sampling on a probability, but we do not know exactly what the probabilities are, only know the relative probabilities of different outcomes (E.g. how much less likely is someone to read this article as compared to being struck by lightning). In this case, we may want to go on to describe change of a certain system instead of absolute outcomes. To do this, we use the Metropolis-Hastings algorithm.

With this variant on Monte Carlo, you begin with a certain configuration, and let every following configuration depend only on the prior configuration. With each Monte Carlo step, you make a random change within your system, from one configuration, say 20 visitors inside a museum, to another configuration, say 21 visitors inside a museum. In order to calculate the probability of this change, you do not need to fret over the precise probability of having 21 visitors. You need only consider how much more likely 21 visitors is as compared to 20.

Of course, as we are the Phyzards, and not the Museumzards, we are more interested in how we may use such an algorithm in physics. Using Metropolis-Hastings, you could for example simulate the behaviour of a gas. At any time, you may have a configuration where the total energy of the gas could start out to be E0. If you want to know the probability that the gas will take on a new configuration with energy E1, you could use the Boltzmann probability, which describes the probability to find a certain energy, to determine the probability of the change occurring. In using this algorithm, you can disregard the normalisation constant, which is quite cumbersome to calculate, and focus only on the easy-to-calculate probability term.

In practice, you may generate a random number, and change your system around if the number is below this probability. In doing so, you are effectively simulating how the gas may evolve with time, with each iteration of your Monte Carlo corresponding with some unit time.

Final remarks

Phew, that was a lot of randomness I just spouted your way. In summary, the Monte Carlo method is a general method for deploying random numbers to do some awesome physics. It can be used for all sorts of stuff, like modelling systems of gasses, integrating functions and even approximating pi.

But this is only the tip of the iceberg when it comes to randomness in physics. From here on out, we will walk a Drunkard’s walk through all the different ways in which randomness rules the foundations of physics.

Stay curious and much love,

Paul Stapel