If you’re reading this blog, you’re probably interested in how Bernoulli’s principle works; either because you heard of it before but don’t know what it is or you need to learn it for your studies. Of course, there is also the possibility of you just wanting to learn more about your favorite household object with some physics thrown in, which is equally valid. Either way, this will be a somewhat shorter and especially sweet post to satisfy your cravings.
One interesting thing to know before we start is that although it’s called Bernoulli’s principle, he only deduced the relations between the properties of water. Once again Euler stepped in, because of course he did, to formulate it in the form that I’ll be describing here.
What is Bernoulli’s principle?
For those who don’t know Bernoulli’s principle, it basically states a relation between the height, pressure and velocity of the water. Using Bernoulli’s principle we can, for example, calculate what the speed would change if a pipe started to narrow after a certain point increasing the pressure. We can do this because we know this relation stays constant, because we know that energy always stays conserved, which is how this relation was originally formulated. Height, pressure and velocity are all forms of energy which could be translated into each other, but of course never dissapear. But I’m getting ahead of myself, so let me first show you the actual formula.
The equation goes like this:
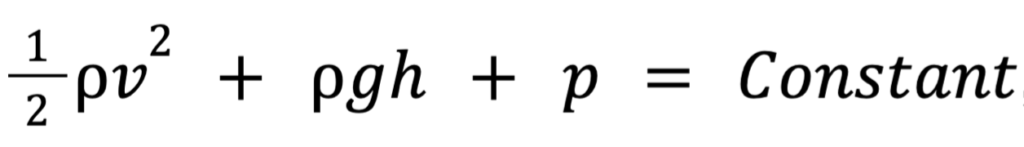
Where rho is density which may be quite different from what you’ve come to expect if you haven’t had the pleasure of doing much with conservation of energy or the ideal gas law. This is because instead of the regular F = ma, where you just fill in a and m and get the force, you’ll have to compare two results to unravel the situation.
So if you had a tube narrowing like I talked about earlier, your starting point is the situation before, where it has a larger pressure. Then you can equate this to the position after, where you know the pressure to be higher, because of the smaller width, but you don’t know the velocity. Then you can fill in all the values you do have, everything except the velocity of the second case, and move the terms around a bunch till you’re left with that which you seek.
So you could also write the equation as:
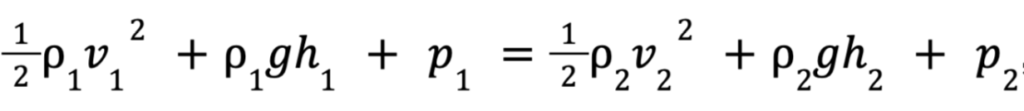
Here the values are denoted as 1 for the first situation and 2 for the second situation. It’s clear why most use the formulation up above, because it’s way easier to write and physicists already don’t like writing a syllable more than they have to (hence all the abbreviations).
VUC; Bernoulli’s bane
With great physics explaining power comes great responsibility, and so does it too for this equation, which can be used in a lot of different situations. When learning something new in physics, it’s equally important to recognise the things that are still left unanswered. In this case that brings us to the three major assumptions which make this principle not a one size fits all. These three are: Viscosity, Unsteadiness and Compressibility or VUC for short.
Viscosity is the measure of the syrupy-ness of a liquid, at least that’s how I like to call it. The formal description is the resistance against deformation, or how long it takes to change its shape. This is one of the things being ignored; it’s assumed that deformation is unresisted, which in real life is never really the case because even water has a viscosity greater than zero.
Then we have the unsteadiness, which is how regular the flow of water is. If the unsteadiness is high it means that the amount of water that passes through a given part changes a lot. Sometimes a lot of water goes through the same part when other times it’s way less.
Compressibility is quite self explanatory, if a large amount of pressure is applied the volume of a liquid decreases. This is akin to what happens with Bernoulli’s principle’s cousin, the ideal gas law.
This is a kind of reminder that the things we learn in physics aren’t actually baked into how the world works, as far as we know at least, but are more models that help us grasp and explain what happens.
However, we can always improve these models for different cases. For all of these drawbacks there are different formulations of our formula that do give really accurate results. Although, in most cases, the standard version is fine enough, because most of the time the wisdom gained is more important than the number our calculator spouts out at us.
I did find out that the Wikipedia page lists most of them though, so if you are dead set on learning everything there is to know about Bernoulli’s principle I’d recommend you start there.
Bernoulli’s colander
However, what can we do with our current version? This is the part where the colander comes into play, which just proves that while straining pasta is the most important use it’s far from the only. The entire reason why I wrote this post is that some time ago, I was cleaning a colander under the sink when something occurred to me. The water started staying at a certain level, even though a lot of it was leaking out through the holes!
So I set out with Bernoulli’s principle in one hand and a colander in the other to try and decipher why this happens and, more interestingly, where it happens.
I will mostly explain how we do this, so there won’t be any calculations, but with my described method it should be relatively doable.
To start things off, it’s very important to relate the volume of the water entering the colander to the velocity. This is pretty easy because of the assumption that flow is steady and incompressible as stated before, meaning that it directly equates to the velocity times the surface area (everything in metric mind you).
You can easily measure or look up the velocity, pressure (+diameter) and height of the faucet. Then you do the same for the colander holes, but in this case you don’t know the velocity and have to go about finding another way to get the pressure. In this case, the applied pressure on the holes would be equal to the standard pressure of the atmosphere (about 1,013 hPa) plus the pressure of the overlying water. While this can be deduced by calculating the weight and dividing it by the surface area of the water, it can be ignored because it is insignificant compared to that of the atmosphere.
Equilibrium
Now let me come clean with you, if you calculate the velocity this way there is a good chance the existing volume is equal or even slightly greater than the entering volume, but how could this even happen? This is because we left out one crucial part, the energy that leaves the system via resistance. This is mostly due to the water pooling up in the colander before being able to drain through the holes. This is why there wouldn’t be an equilibrium like this if the holes were directly connected to the faucet via tubes. This is also why, when you use a model like Bernoulli’s principle, you must always continue to think about what the model doesn’t include when you relate it to real life.
But if we take into account resistance, or at least look at when the escaping volume is lower than that of which enters, we would expect the volume within the colander to continue to grow. This is because the difference between the two is also in volume per second and so it should increase every second. So how come we still get an equilibrium? This is because the number of holes that the water comes in contact with keeps increasing and so there is more total volume being lost. This is why the equilibrium will always be on or, most likely, at the bottom of a new row of holes in the colander, if not the first one.
An overview
I’ve made a simple yet robust diagram (not to scale) for you to more easily intuit what’s happening here:
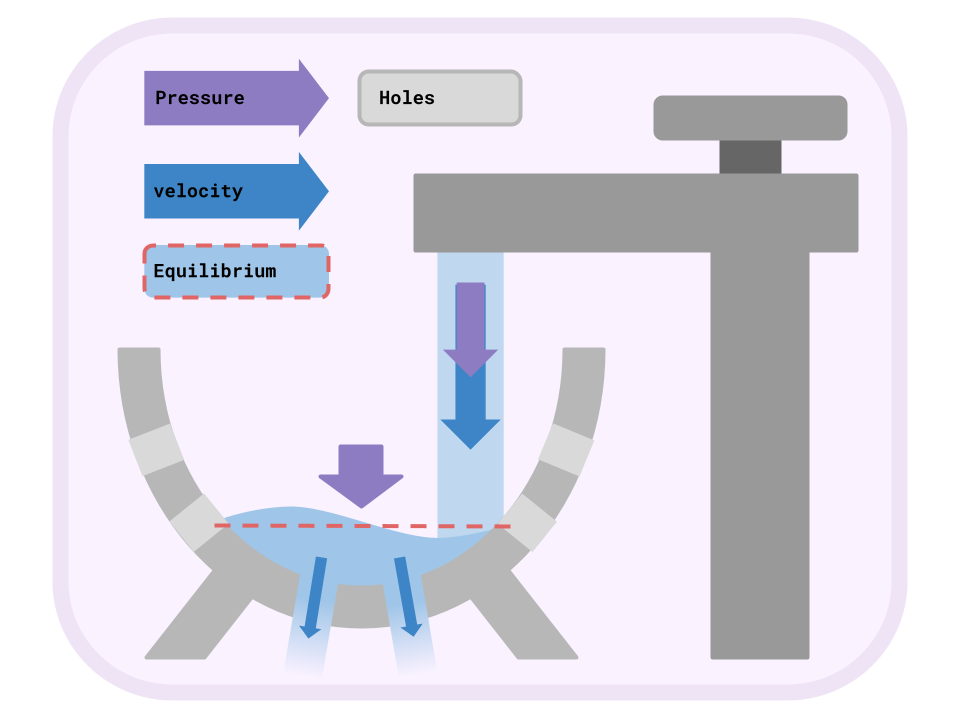
Here you can see the water entering through the faucet with a high speed and pressure, then it pools up in the colander. From here it has the standard surface pressure on top of it and moves through the holes with a larger velocity. This is because the pressure and height have decreased from the start of the faucet, meaning that for the equation to stay constant the velocity must increase. Then a smaller volume than the entering volume leaves through the bottom holes allowing the excess water to pool up in the colander until it reaches the next layer of holes. Here the difference between velocities and surface areas high enough where it continues this whole chain of events until the next layer or it reaches equilibrium.
Final remarks
If the subject of this blog interests you, you could easily try to verify what I said here by looking the values up, measuring your home setup and then putting your colander under the faucet. I of course have also done it and this is partially how I verified what would happen, but peer review is always important and in this case also fun.
That was it for this blog, but much more about water and water and water and water and pasta may come soon in another blog! who knows? (well, I do)

0 Comments