Lately, I’ve been finding some joy in riddles and paradoxes. I’ve read up on some physics related ones, and stumbled upon a particularly baffling example, popularised by one of my favourite physicists Richard Feynman. Let me lay out the scenario for you:
Suppose you have an S-shaped sprinkler atop a pivot (see figure below). The sprinkler should be able to rotate along the axis of this pivot! When you turn on this contraption, the sprinkler will push out water, and this water will in turn push back against the sprinkler. This will, naturally, make the sprinkler start rotating backwards (colored in blue).
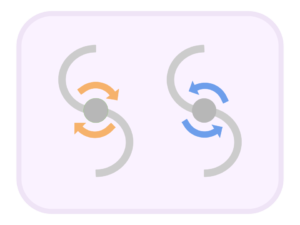
Now, the question is: what would happen if you were to submerge the sprinkler in water and make it suck up the water instead of pushing it out?
There are three possiblities:
-
- It will rotate forwards.
-
- It will rotate backwards.
-
- It won’t rotate at all.
Just like Feynman did back when he stumbled upon this paradox. I will give you an argument for each case.
An argument for rotating forwards
OK, so when the sprinkler starts sucking up water, what really happens is that the water will be pulled into the sprinkler. Because of this, the sprinkler is exerting a force on this water so as to pull it towards itself. As we know, every force is accompanied by an opposing and equal force. This means that once the sprinkler starts pulling on the water, the water will also pull the sprinkler forwards. This would make the sprinkler start rotating forwards.
Let me give you an analogy:
Imagine you’re on roller-skates, and there’s a rope with one end attached to a wall, and the other in your hand. Once you start to pull in the rope, you would also be pulling yourself towards the wall. That’s what would happen to the sprinkler pulling in the water.
An argument for rotating backwards
Let’s look at this problem another way. When you suck up the water into the nozzle of the sprinkler, the water will flow in perpendicular to the nozzle of the sprinkler. From that point on, the water would need to flow into the nozzle. This means that the perpendicular velocity would need to be negated, and then a velocity into the nozzle needs to be given to the water. The negation of the perpendicular velocity requires a force exerted by the sprinkler. This force comes with an opposite force on the sprinkler, and this makes the sprinkler rotate backwards.
Let me give you an analogy:
Imagine you are, once again, on roller-skates (look at you, grooving it out 
But why not both!?
So we have looked at two possible explanations giving opposite results, but they need not be mutually exclusive. If both were to occur at the same time, then one could argue that the sprinkler would not move forwards or backwards, but stand completely still. Of course, there is some subtlety to this. Because the pulling needs to accelerate the water, and that accelerated water needs to slow down again to a same degree. This might suggest that the forces to accelerate and decelerate should be equal, and thus that the forces on the sprinkler should also be equal and opposite. Some observations, like those of Feynman and Ernst Mach, have shown this to be the case.
Fluids, however, are not ideal, and so these observations only occur in rare cases where the suction is weak and so the water will flow slowly. Slow flowing liquid will have a so called laminar flow, with a low convection, so that momentum loss will be kept to a minimum. When the liquid flows more quickly, however, it will have a turbulent flow, and may cause vortices to appear within the water.
In case of this turbulent flow, these vortices will make it so that the water will lose momentum in the perpendicular direction, so that the overall forward force it got from pulling te water in would be slightly larger than the backwards kick from the water hitting it. This means that, if the water is flowing fast enough, you will see the sprinkler slowly start to move forwards.
Our final answer
So, if the suction is low, the reverse sprinkler will not move at all, and if the suction is high, it will start rotating forwards. That means that you can rest easy knowing this paradox has been solved.
But wait! There is still more science to be done 
Say I where to add another S-shaped sprinkler on top of the old sprinkler, so our sprinkler system now contains two equal, stacked sprinklers attached to each other. Outside of the water, the sprinkler would output twice the force and have twice the mass, so that it would still rotate as quickly as usual. But will this new system also work the same when we submerge it in water and start sucking? Will the direction of rotation change? What about the angular velocity?
Feel free to share your thoughts and discuss in the comments below
Follow our Astronomicon for the answer, along with more physics goodness. Stay curious, stay hydrated, and enjoy your week!
Paul Stapel
Student
I’m an aspiring writer, teacher, wizard and physicist!
Stats
Future
55%
Past
45%

0 Comments